基础概念

算法定义

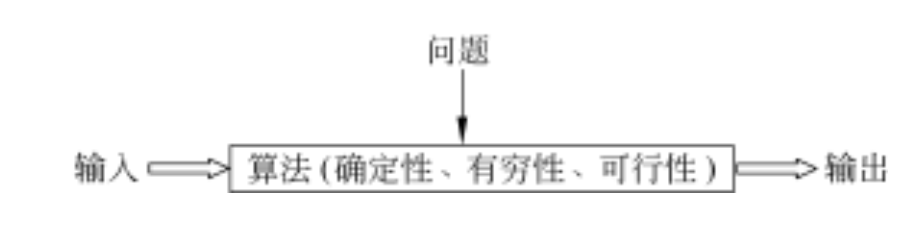
算法（algorithm)是解决问题的方法。严格地说，算法是对特定问题求解步骤的一种描述，是指令的有限序列，此外算法还必须满足下列5个重要特性：
（1）输入：一个算法有另个或多个输入。算法的输入有两种方式：一种是从外界获得数据，另一种是由算法自己产生并被处理的数据。
（2）输出：一个算法有一个或多个输出。既然算法是为解决问题二设计的，算法实现的最终目的就是要获得问题的解。没有输出的算法是无意义的。
（3）有穷性：一个算法必须总是（对任何合法的输入）再执行有穷步之后结束，且每一步都在有穷时间内完成。
（4）确定性：算法终的每一条指令必须有确切的含义，不存在二义性。并且，在任何条件下，对于相同的输入只能得到相同的输出。
（5）可行性：算法描述的操作可以通过已经实现的基本做执行有限次来实现。

算法的描述方法

算法的描述方法有自然语言、流程图、程序设计语言和伪代码等。
用自然语言描述算法，最大的优点是容易理解，缺点是容易出现二义性，并且算法通常很冗长。
用流程图描述算法，优点是直观易懂，缺点是严密性不如程序设计语言，灵活性不如自然语言。在计算机早期应用中，使用流程图描述算法占统治地位，但实践证明，除简单算法外，这种描述方法使用起来非常不方便。
程序设计语言描述的算法能由计算机直接执行，而缺点是抽象性差，使算法设计者拘泥于算法描述的具体细节，忽略了好算法的正确逻辑的重要性，此外，还要求算法设计者掌握程序设计语言及编程技巧。
伪代码(pseudocode)是介于自然语言和程序设计语言之间的方法，它采用某一程序设计语言的基本语法，操作指令可以结合自然语言来设计。伪代码不是一种实际的编程语言，但在表达能力上类似于编程语言，同时及消化了描述算法的不必要的技术细节。

算法设计的一般过程

理解问题
在设计算法时首先需要做的第一件事是完全理解要解决的问题，仔细阅读要处理的问题，并收工处理一些小例子。
预测所有可能的输入
算法的输入确定了该算法所解问题的一个实例。预测算法的可能的输入，包括合法的输入和非法输入。
在精确解和近似解间做选择
有些问题无法求得精确解，例如平方根、解非线性方程等，有些问题有其固有的复杂性，求精确解需要花费太长时间，如旅行商问题（TSP问题，指旅行家要旅行n个城市，要求经历各个城市且仅经历一次，并要求所走的路程最短）。有时需要根据问题以及问题所受的资源限制，在精确解和近似解间做选择。
确定适当的数据结构
算法设计技术
算法设计技术（algorithm design technique,也称算法设计策略)是设计算法的一般性方法。包括蛮力法，分治法，减治法，动态规划法，贪心法，分支限定法，概率算法，近似算法等。
描述算法
跟踪算法
分析算法的效率
根据算法编写代码

重要问题类型

查找问题

排序问题

图问题

算法分析

渐进符号

基本语句（basic statement）是执行次数与整个算法的执行次数成正比的语句，基本语句对算法运行时间的贡献最大，是算法中最重要的操作。这种衡量效率的方法得出的不是时间量，而是一种增长趋势的度量。换言之，只考察当问题规模充分大时，算法中基本语句的执行次数在渐进意义下的阶，通常用大O，大Ω和Θ三种渐进符号表示。

大O符号

定义若存在两个正的常数$c$和$n_0$，对于任意$n \ge n_0$,都有$T(n) \le c \ast f(n)$, 则称$T(n) = O(f(n))$（或称算法在O(f(n))中）。
大O符号用来描述增长率的上限，表示T(n)的增长最多像f(n)增长的那样快，也就是说，当输入规模为n时，算法消耗时间的最大值，这个上限的阶越低，结果就越有价值。

大$\Omega$

定义若存在两个正的常数和$n_0$,对于任意$n \ge n_0$,都有$T(n) \ge c \ast g(n)$, 则称$T(n) = \Omega(g(n))$(或称算法在$\Omega(g(n))$中)。
大$\Omega$符号用来描述增长率的下限，也就是说，当输入规模为n时，算法消耗时间的最小值。与大O符号对称，这个下限的阶越高，结果就越有价值。
大$\Omega$符号常常与大O符号配合以证明某问题的一个特定算法是该问题的最优算法，或是该问题中的某类算法中的最优算法。

$\Theta$符号

定义若存在三个正的常数$c_1$，$c_2$和$n_0$，对于任意$n \ge n_0$，都有$c_1 \ast f(n) \ge T(n) \ge c_2 \ast f(n)$,则称$T(n) = \Theta(f(n))$。
$\Theta$符号意味着T(n)与f(n)同阶，用来表示算法的精确阶。
定理若$T(n)=a_mn^m+a_m-1n^m-1+...+a_1n+a_0(a_m \gt 0)$，则有$T(n)=O(n^m)$,且$T(n)=\Omega(n_m)$，因此,有$T(n)=\Theta(n^m)$。

经典例子

求最大公约数

求最大公约数最常用的算法即为欧几里得算法，也称辗转相除法。
利用的性质：

若r是a÷b的余数，则gcd(a,b)=gcd(b,r)
a和其倍数的最大公约数为a

证明：

令c=gcd(a,b) a>=b
令r=a mod b 设a=kc,b=jc，则k,j互素，否则c不是最大公约数
r = a - mb = kc - mjc = (k-mj)c，即r也是c的倍数，且k-mj与j互素，否则与前述k,j互素矛盾，由此可知b与r的最大公约数也是c,即gcd(a,b) = gcd(b, a mod b) 得证。

注: gcd(greatest common divisor,最大公约数)缩写。

实现方式一: 穷举法
穷举法是解决算法问题最"野蛮"的一种方法，但是有些时候也很有效，在规模不大和对效率要求不高的情况下用的较多。直接给出实现：

int gcd(int a, int b)
{
    int i = 0;

    for(i = 1; i <= b; i++)
    {
        if((a%i == 0) && (b%i == 0))
            return i;
    }
}

实现方式二: 非递归实现

int gcd(int a , int b)
{
    int c = a % b；

    while(c)
    {
        a = b;
        b = c;
        c = a % b;
    }

    return b;
}

实现方式三: 递归实现

使用递归方式实现求最大公约数，将问题定义为求i和j的最大公约数gcd(i,j)，其中i和j是整数，且i>=j。算法的地柜表示如下：
1.若j能整除i，那么gcd(，j) = j;
2.j不能整除i, 令r=i mod j, 那么gcd(i,j) = gcd(j, r)

int gcd(int i, int j)
{
    int r = i % j;
    return r == 0 ? j : gcd(j, i);
}

参考资料

1.http://blog.csdn.net/fly_yr/article/details/50764286
2.《算法设计与分析》清华大学出版社