[TOC]

下界

  对于任何待求解的问题，如果能找到一个尽可能大的函数g(n)(n为问题规模)，使得求解该问题的所有算法都可以在$\Omega(g(n))$的时间内完成，则称函数g(n)为该问题计算复杂性的下界(lower bound)。如果已经知道一个和下界的效率类型相同的算法，则称该下界是紧密(close)的。

平凡下界

  确定一个问题的计算复杂ing下界的最简单方法是对问题的输入中必须要处理的元素进行计数，同时，对必须要输出的元素进行计数。因为任何算法至少要“读取”所有要处理的元素，并“写出”它的全部输出，这种计数方法产生的是一个平凡下界（ordinary lower bound)。平凡下界往往过小而没有意义。

判定树模型

  判定树（decision trees)是这样一棵二叉树：它的每一个内部节点对应一个形如$x \leq y$的比较，如果关系成立，则控制转移到该节点的左子树，否则，控制转移到该节点的右子树，它的每一个叶子节点表示问题的一个结果。在用判定树模型建立问题的时间下界时，通常忽略求解问题的所有算数运算，只考虑分支执行时的转移次数。
引理：  若T是至少具有n!个叶子节点的二叉树,则T的高度至少是:

    nlog_2n - 15n = \Omega(nlog_2n)

  该引理通常称为信息论下界，它说明任何基于比较的对n个元素排序的算法，判定树的高度都不会大于$\Omega(nlog_2n)$，因此，$\Omega(nlog_2n)$是这些算法的下界。因此，右下面的定理：
定理： 任何基于比较的排序算法，对n个元素进行排序的时间下界为$\Omega(nlog_2n)$。

最优算法

  所谓最优算法(optimality algorithm)是指在某一种度量标准下，优于该问题的所有(可能的)的算法。一般情况下，如果能够证明求解问题$\Pi$的任何算法的运行时间下界是$\Omega(g(n))$，那么，对以时间$\Omega(g(n))$来求解问题$\Pi$的任何算法，都认为是最优算法。

算法的极限

易解问题与难解问题

  在计算机科学界已达成这样的共识：把多项式时间复杂性作为易解问题和难解问题的分界线。

P类问题和NP类问题

判定问题

  一个判定问题（decision problem)是仅仅要求回答yes或no的问题。判定问题有一个重要特性：虽然在计算上对问题求解是困难的，但在计算上判定一个待定解是否解决了该问题却是简单的。

确定算法与P类问题

定义  设A是求解问题$\Pi$的一个算法，如果在算法的整个执行过程中，每一步只有一个确定的选择，则称算法A是确定性（determinism)算法。
  确定性算法在执行过程中，每一个步骤都有一个确定的选择，如果重新用同一输入实例运行算法，所得的结果严格一致。
定义如果对于某个判定问题$\Pi$，存在一个非负整数k,对于输入规模为n的实例，能够以$\Omega(n^k)$的时间运行一个确定性算法，得到yes或no的答案，则该判定问题是一个P(polynomial)类问题。
  P类问题是由具有多项式时间的确定性算法来求解的判定问题组成。对于判定问题定义P类问题，主要是为了能够给出较为严格的NP类问题的定义。所有易解问题都属于P类问题。

非确定性算法与NP类问题

定义 设定A是求解问题$\Pi$的一个算法，如果算法A以如下猜测并验证的方式工作，就称算法A是非确定性（nondeterminism）算法：
（1）猜测阶段。在这个阶段，对问题的输入实例产生一个任意字符串Y，在算法的每一次运行时，串y的值可能不同，因此，猜测以一种非确定的形式工作。
（2）验证阶段。在这个阶段，用一个确定性算法验证两件事：首先，检查在猜测阶段产生的串y是否是合适的形式，如果不是，则算法停下来并得到no；另一方面，如果串y是合适的形式，那么算法验证它是否是问题的解，如果是问题的解，则算法停下来并得到yes，否则，算法停下来并得到no。
定义&msp; 如果对于某个判定问题$\Pi$,存在一个非负整数k，对于输入规模为n的实例，能够以$Omega(n^k)$的时间运行一个非确定性算法，得到yes或no的答案，则该判定问题$\Pi$是一个NP(nondeterministic polynomial)类问题。
  对于NP类判定问题，重要的是它必须存在一个确定性算法，能够以多项式时间来检查和验证在猜测阶段所产生的答案。
  P类问题和NP类问题的主要差别在于：
(1)P类问题可以用多项式时间的确定性算法来进行判定或求解；
(2)NP类问题可以用多项式时间的非确定性算法来进行判定或求解。

NP完全问题

  NP完全问题是NP类问题的一个子类，对合格子类中的任何一个问题，如果能够证明用多项式时间的确定性算法进行求解或判定，那么，NP完全问题中的所有问题都可以通过多项式时间的确定性算法来进行求解或判定。

问题变换与计算复杂性规约

定义 假设问题$\Pi'$存在一个算法A，对于问题$\Pi'$的输入实例$I'$，算法A求解问题\Pi'得到一个输出$O'$，另外一个问题$\Pi$的输入实例是$I$,对应于输入$I$，问题$\Pi$有一个输出O，则问题$\Pi$变换到问题$\Pi'$是一个3个步骤的过程：
(1)输入转换：把问题$\Pi$的输入I转换为问题\Pi'的适当输入$I'$
(2)问题求解：对问题$\Pi'$应用算法A产生一个输出$O'$
(3)输出转换：把问题$\Pi'$的输出$O'$转换为问题Pi对应于输入$I$的正确输出。

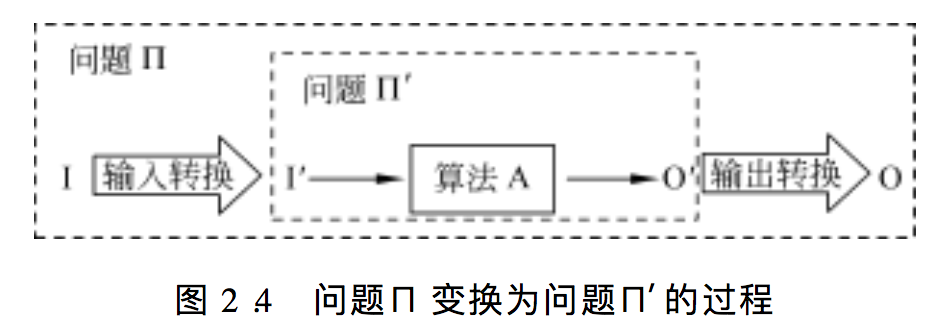
  若在$O(\tau(n)) $的时间内完成上述输入和输出转换，则称问题$\Pi$以$\tau(n)$时间变换到问题$\Pi'$,记为$\Pi\propto_{\tau(n)}\Pi'$,其中，n为问题规模；若在多项式时间内完成上述输入和输出转换，则称问题$\Pi$以多项式时间变换到问题$\Pi'$，记为$\Pi \proptop \Pi'$。
定理 （计算时间下限规约) 若已知问题$\Pi$的计算时间下限是$T(n)$,且问题$\Pi$
可以$\tau(n)$变换到问题$\Pi'$，即$\Pi\propto{\tau(n)}\Pi'$,则$T(n)-O( \tau(n))$为问题$\Pi'$的一个计算时间下限。
定理 (计算时间上限规约)若已知问题$\Pi$的计算时间下限是$T(n)$,且问题$\Pi$
可以$\tau(n)$变换到问题$\Pi'$，即$\Pi\propto_{\tau(n)}\Pi'$,则$T(n)+O( \tau(n))$为问题$\Pi$的计算时间上限。
  多项式问题变换是可以传递的。

NP完全问题的定义

定义 令$\Pi$是一个判定问题，如果问题$\Pi$属于$NP$类问题，并且对NP类问题的每一个问题$Pi'$，都有$\Pi' \propto_p \Pi$,则称判定问题N是一个NP完全问题（NP complete problem)，优势把NP完全问题记为NPC。