[笔记]分治法 – 知新小筑

分治者，分而治之也（感觉有点废话）。分治法（divide and conquer method)是最著名的算法设计技术，作为解决问题的一般性策略，分治法在政治和军事领域也是克敌制胜的法宝。

概述

分冶法的设计思想是将一个难以直接解决的大问题，划分成一些规模较小的子问题，以便各个击破，分而治之。更一般地说，将要求解的原问题划分成k个较小规模的子问题，对这k个子问题分别求解。如果子问题的规模仍然不够小，则再讲每个子问题划分为k个规模更小的子问题，如此分解下去，直到问题规模足够小，很容易求出其解为止，再将子问题的解合并为一个更大规模的问题的解，自底向上逐步求出原问题的解。
人们从大量实践中发现，在用分冶法设计算法时，最好使子问题的规模大致相等。也就是将一个问题划分成大小相等的k个子问题（通常k=2),这种使子问题规模大致相等的做法是出自一种平衡子问题的思想，它几乎总是比及问题规模不等的做法要好。另外，在用分冶法设计算法时，最好使各各子问题之间相互独立，这涉及分冶法的效率。如果各子问题不是独立的，则分冶法需要重复地求解公共的子问题，此时虽然也可以用分冶法，但一般用动态规划法较好。
分冶法典型情况：

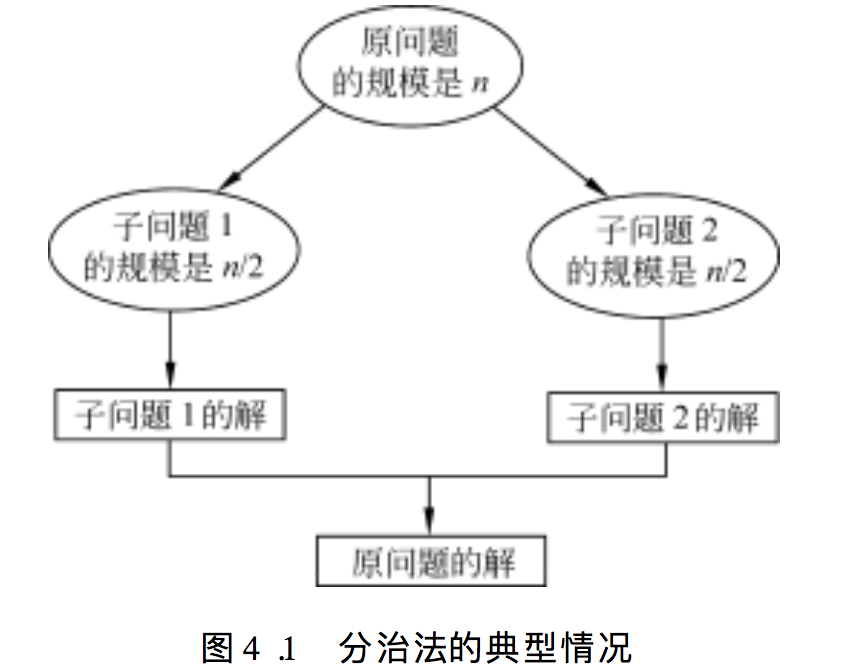
分治法的求解过程

（1）划分：把规模为n的原问题划分为k个规模较小的子问题，并尽量使这k个子问题的规模大致相等。
（2）求解子问题：各子问题的解法与原问题的解法通常是相同的，可以用递归的方法求解各个子问题，有时递归也可以用循环来实现。
（3）合并：把各个子问题的解合并起来，合并的代价因情况不同有很大差异，分冶算法的有效性很大程度上依赖于合并的实现。
分冶法的一般过程:

DivideConquer(P)
{
    if(P的规模足够小)
        直接求解P
    分解为k个子问题p1,p2,p3..pk;
    for(i = 1; i <=k; i++)
        yi=DivideConquer(Pi);//解决各子问题，通常采用递归

    return Merge(y1,...,yk)；//将各子问题的解合并为原问题的解
}

书中举了个计算$a^n$的例子，其采用分治法的时间复杂度为$O(nlog_2n)$，而蛮力法为$O(n)$。说明不是所有的分治法都比简单的蛮力法更有效，但是，正确使用分治法往往比其他算法设计方法的效率更高。

递归

递归的两个基本要素：
(1)边界条件：确定递归到何时终止，也称之为递归出口；
(2)递归模式：大问题是如何分解为小问题的，也称为递归体。
递归函数只有具备了这两个要素，才能在有限次计算后得出结果。
最典型的就是汉诺塔了。
汉诺塔的三个步骤实现：
(1)将塔A上的n-1个碟子借助塔C先移到塔B上；
(2)把塔A上剩下的一个碟子移到塔C上；
(3)将n-1个碟子从塔B借助塔A移到塔C上

void Hanoi(int n, char A, char B， char C)
{
    if(n==1)
        Move(A,C); //Move是一个抽象操作，表示将碟子从A移到C
    else
    {
        Hanoi(n-1, A, C,B);
        Move(A,C);
        Hanoi(n-1,B,A,C);
    }
}

排序问题中的分冶法

归并排序

二路归并排序是成功应用分治法的一个完美的例子：

//将r[s..t]归并排序为r[s..t],r1为中间变量
void MergeSort(int r[], int r1[], int s, int t)
{
    if(s == t)
        r1[s] == r[s];
    else
    {
        m = (s+t)/2;
        MergeSort(r,r1,s,m);//归并排序前半个子序列
        MergeSort(r,r1,m+1,t)；//归并排序后半个子序列
        Merge(r1,r,s,m,t);
    }
}

合并方法：

void Merge(int r[],int r1[],int s,int m, int t)
{
    i = s; j = m+1; k=s;
    while(i <= m && j <= t)
    {
        //取r[i]和r[j]中较小者放入r1[k]
        if(r[i] <= r[j])
        {
            r1[k++] = r[i++];
        }
        else
        {
            r1[k++] = r[j++];
        }
    }

    //若第一个子序列没处理完，则进行收尾处理    
    if(i <= m)
    {
        while(i <= m)
        {
            r1[k++] = r[i++];
        }
    }
    else
    {
        //若第二个子序列没处理完，则进行收尾处理
        whiel(j <= t)
        {
            r1【k++] = r[j++];
        }
    }

}

在实际使用中可以通过：

MergeSort(arr,tmp_arr,1,len);//索引从1开始，tmp_arr为中间过程申请的内存。

二路归并排序算法的时间代价是$O(nlog_2n)$。二路归并排序在合并过程中需要与原始记录序列同样数量的存储空间，因此其时间复杂度是$O(n)$

快速排序

快速排序也是基于分治技术的重要排序算法，和归并排序不同的是：归并排序是按照记录在序列中的位置对序列进行划分的，而快速排序是按照记录的值对序列进行划分的。

//分开r[first..end]并返回处理后的中间值，这种处理方式可以将每次的partition
//尽量保持在中间位置
int Partition(int r[], int first, int end)
{
    i = first;
    j = end;

    while(i < j)
    {
        //右侧扫描
        while(i < j && r[i] <= r[j])
        {
            j--;
        }

        if(i < j)
        {
            r[i]与r[j]交换;//将较小记录交换到前面
            i++；
        }

        //左侧扫描
        while(i < j && r[i] <= r[j])
        {
            i++;
        }

        if(i < j)
        {
            r[j]与r[i]交换;//将较大记录交换到后面
            j--;
        }
    }

    return i; //i为轴值记录的最终位置
}
void QuikSort(int r[], int first, int end)
{
    if(first < end)
    {
        pivot = Partition(r, first, end); //问题分解，pivot是轴值在序列中的位置
        QuikSort(r,first, pivot-1);//递归地对左侧序列进行快速排序
        QuikSort(r,pivot+1, end)；//递归地对右侧子序列进行快速排序
    }
}

快速排序的时间复杂度也是$O(nlog_2n)$，但是不需要归并排序的临时空间，为就地排序算法。

组合问题中的分治法

最大字段和问题

文中给出的定义很长，这里就不抄了，例如，序列（-20，11，-4，13，-5，-2）的最大子段和为2到4的为20。若所有的值君小于0，则最终结果为0。

int MaxSum(int a[], int left, int right)
{
    sum = 0;
    if(left == right)
    {
        //序列长度为1，直接求解
        if(a[left] > 0)
            sum = a[left];
        else
            sum = 0;
    }
    else
    {
        center = (left+right)/2; //划分
        leftsum = MaxSum(a, left, center); //前半段递归求取最大子序列
        rightsum = MaxSum(a, center+1, right); //后半段递归求解求取最大子序列
        //计算跨中间界的最大子序列
        s1 = 0; 
        lefts = 0;
        for(i = center; i>=left; i--)
        {
            lefts += a[i];
            if(lefts > s1) 
                s1 = lefts;
        }

        s2 = 0;
        rights = 0;
        for(j = center+1; j <= right; j++)
        {
            rights += a[j];
            if(rights > s2)
                s2 = rights;
        }

        sum = s1 + s2; //计算跨域时的最大子段和
        if(sum < leftsum)
            sum = leftsum;
        if(sum < rightsum)
            sum = rightssum；
    }

    return sum;
}

概述